Square Root algorithm for C

CodeProject

Introduction

For those who are looking for how square root algorithm is working and “YES !, Welcome to my blog”, but for those who are simply looking for performing square root your programming and I have to tell you, what you have to do is do some google searching on “math.h” header file to look for square root function that prepared inside it.
Well, let’s begin our lesson “How square root algorithm is working on c”
It’s not very difficult once you have understand how following equation is calculated
Left hand side of the diagram shows the square root of 152.2756 and right hand side shows the square root of 2.
For those who have understand how this calculation is been done, please skip to the code as I am going to explain the how to solve this equation.

Basic Principle of Square Root

Based on the question given above, we understand that square root of 152.2756 is 12.34 and the square root of 2 is 1.4142. If you do not believe, try calculator to find the answer.
Suppose we are finding the square root of 2 and the answer is 1.4142. We can expressed it such that

If we expressed it to algebra expression as following.

Suppose a is continue for n times, it can be expressed as following
Why I am treating it continue as n times but not 5 times? Because we cannot ensure that all positive number will give us a 5 digits answer after square root it. So we have to suppose there are n digits after square root.
Right-hand-side term can be expanded as following

From the equation above, we can understand square root equation can be solved by following equation.
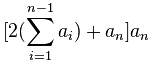The most important rule of this equation is we pick a number from 1,2,3,4,5,6,7,8,9 and multiple it with 10^m, where m = Integer (exp. 3,2,1,0,-1,-2,-3,...) and substitute into  that must be smaller then the number we are going to minus or equal to it. It’s the most difficult part on square-root equation so lets understand it by solving square root of 2.

So, from the solution above, we understand that

And we sum up all the value, we get the answer 1.414 approximate to 1.4142

Algorithm

Based on the method above, what kind of works should we applied on algorithm as following

• Create equation 
• Create function of power of ten
• Find suitable number that bigger then 0 for variable a from loop
• Find suitable number that smaller then 0 but positive for variable a from loop
• Sum all variable a and return it as double

First, we are going to create the equation as we mentioned above

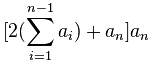
We can expressed it as code as following

(( 2 * rst ) + ( j * powerOfTen(i)))*( j * powerOfTen(i))

where rst and j is declared as double and i is int. powerOfTen is a function that return a value of i times multiple of 10.

It’s code of function powerOfTen

  1: 
  2: double powerOfTen(int num){
  3:      double rst = 1.0;
  4:      if(num >= 0){
  5:           for(int i = 0; i < num ; i++){
  6:                rst *= 10.0;
  7:           }
  8:      }else{
  9:           for(int i = 0; i < (0 - num ); i++){
 10:                rst *= 0.1;
 11:           }
 12:      }
 13: 
 14:      return rst;
 15: }

We have to judge that variable a must be smaller then upper number. It’s how it looks like

if(z - (( 2 * rst ) + ( j * powerOfTen(i)))*( j * powerOfTen(i)) >= 0)

where z  is declared as double and treat as upper number.

There are two loops, one loop for finding the suitable number from 10000,1000,100,10… and another one loop for find suitable number from 1,2,3,4,5…

  1: for(i = max ; i > 0 ; i--){
  2:      // value must be bigger then 0
  3:      if(z - (( 2 * rst ) + ( j * powerOfTen(i)))*( j * powerOfTen(i)) >= 0)
  4:      {
  5:           while( z - (( 2 * rst ) + ( j * powerOfTen(i)))*( j * powerOfTen(i)) >= 0)
  6:           {
  7:                j++;
  8:                if(j >= 10) break;
  9:                     
 10:           }
 11:           j--; //correct the extra value by minus one to j
 12:           z -= (( 2 * rst ) + ( j * powerOfTen(i)))*( j * powerOfTen(i)); //find value of z
 13: 
 14:           rst += j * powerOfTen(i);     // find sum of a
 15:                
 16:           j = 1.0;
 17:           
 18: 
 19:      }          
 20: 
 21: }

Same loop as above but this times we are going to find the decimal number.

  1: for(i = 0 ; i >= 0 - max ; i--){
  2:      if(z - (( 2 * rst ) + ( j * powerOfTen(i)))*( j * powerOfTen(i)) >= 0)
  3:      {
  4:           while( z - (( 2 * rst ) + ( j * powerOfTen(i)))*( j * powerOfTen(i)) >= 0)
  5:           {
  6:                j++;
  7:                if(j >= 10) break;                    
  8:           }
  9:           j--;
 10:           z -= (( 2 * rst ) + ( j * powerOfTen(i)))*( j * powerOfTen(i)); //find value of z
 11: 
 12:           rst += j * powerOfTen(i);     // find sum of a               
 13:           j = 1.0;
 14:      }
 15: }

This is how the whole squareRoot algorithm looks like

  1: double squareRoot(double a)
  2: {
  3:      /*
  4:           find more detail of this method on wiki methods_of_computing_square_roots
  5: 
  6:           *** Babylonian method cannot get exact zero but approximately value of the square_root
  7:      */

  8:      double z = a;     

  9:      double rst = 0.0;

 10:      int max = 8;     // to define maximum digit 

 11:      int i;

 12:      double j = 1.0;

 13:      for(i = max ; i > 0 ; i--){

 14:           // value must be bigger then 0

 15:           if(z - (( 2 * rst ) + ( j * powerOfTen(i)))*( j * powerOfTen(i)) >= 0)

 16:           {

 17:                while( z - (( 2 * rst ) + ( j * powerOfTen(i)))*( j * powerOfTen(i)) >= 0)

 18:                {

 19:                     j++;

 20:                     if(j >= 10) break;

 21:                     

 22:                }

 23:                j--; //correct the extra value by minus one to j

 24:                z -= (( 2 * rst ) + ( j * powerOfTen(i)))*( j * powerOfTen(i)); //find value of z

 25: 

 26:                rst += j * powerOfTen(i);     // find sum of a

 27:                

 28:                j = 1.0;

 29:           

 30: 

 31:           }          

 32: 

 33:      }

 34: 

 35:      for(i = 0 ; i >= 0 - max ; i--){

 36:           if(z - (( 2 * rst ) + ( j * powerOfTen(i)))*( j * powerOfTen(i)) >= 0)

 37:           {

 38:                while( z - (( 2 * rst ) + ( j * powerOfTen(i)))*( j * powerOfTen(i)) >= 0)

 39:                {

 40:                     j++;

 41:                     if(j >= 10) break;                    

 42:                }

 43:                j--;

 44:                z -= (( 2 * rst ) + ( j * powerOfTen(i)))*( j * powerOfTen(i)); //find value of z

 45: 

 46:                rst += j * powerOfTen(i);     // find sum of a               

 47:                j = 1.0;

 48:           }

 49:      }

 50:      // find the number on each digit

 51:      return rst;

 52: }

 53: 

Reference

I am referring to this wiki website. For more details, please refer on this website. Thank you.